Bạn đã từng nghe rằng Python có thể được sử dụng như một chiếc máy tính bỏ túi linh hoạt? Thậm chí còn hơn thế nữa, với một loạt các thư viện và chức năng chuyên biệt, Python có thể biến thành một máy tính khoa học hoặc thậm chí là máy tính đồ thị mạnh mẽ, vượt trội hơn hẳn các thiết bị cầm tay truyền thống về khả năng và tính linh hoạt.
Trong vai trò là một chuyên gia SEO và biên tập viên cấp cao của tinhoccongnghe.net, chúng tôi cam kết mang đến cho độc giả Việt Nam những hướng dẫn công nghệ uy tín và dẫn đầu. Bài viết này sẽ đi sâu vào cách bạn có thể tận dụng sức mạnh của Python để thực hiện từ những phép tính toán học cơ bản đến phức tạp, từ đại số, lượng giác, thống kê cho đến giải phương trình và vẽ đồ thị. Hãy cùng khám phá những khả năng đáng kinh ngạc mà Python mang lại, giúp bạn tối ưu hóa công việc học tập và nghiên cứu một cách hiệu quả nhất, loại bỏ sự phụ thuộc vào các máy tính cầm tay truyền thống.
1. Tính toán lũy thừa, căn bậc và logarit với Python
Các phép tính lũy thừa, căn bậc và logarit là những thao tác toán học cơ bản nhưng vô cùng quan trọng, và Python cung cấp cách thực hiện chúng một cách đơn giản và hiệu quả. Các hàm này là lý do chính khiến Python trở thành một lựa chọn thay thế tuyệt vời cho máy tính khoa học cầm tay.
Lũy thừa: Sử dụng toán tử **
Để nâng một số cơ sở lên lũy thừa n, bạn chỉ cần sử dụng toán tử **. Ví dụ, để tính 2 mũ 2:
2**2Kết quả sẽ là 4. Điều này có thể hơi khác so với các ngôn ngữ hoặc phần mềm khác như Excel, nơi toán tử ^ (caret) thường được dùng cho lũy thừa. Nếu bạn gặp lỗi, hãy đảm bảo rằng bạn đã sử dụng đúng toán tử ** trong Python.
Căn bậc: math.sqrt() và **(1/n)
Tính căn bậc hai cũng rất đơn giản với thư viện math của Python. Hàm math.sqrt() sẽ trả về căn bậc hai của một số:
import math
math.sqrt(81)Thao tác này sẽ trả về số 9. Đối với các số không phải là số chính phương, nó sẽ trả về một giá trị thập phân xấp xỉ, giống như một máy tính khoa học cầm tay. Ngoài ra, hàm math.cbrt() (có sẵn từ Python 3.11) hoạt động tương tự cho căn bậc ba.
Để lấy căn bậc cao hơn 3 (ví dụ căn bậc n), bạn có thể nâng số đó lên lũy thừa 1/n bằng cách sử dụng toán tử lũy thừa **. Ví dụ, để lấy căn bậc tám của 256:
256**(1/8)Dấu ngoặc đơn (1/8) là rất quan trọng để Python hiểu rằng bạn muốn tính lũy thừa phân số. Nếu không có ngoặc, Python sẽ tính 256 mũ 1 (bằng 256), sau đó chia cho 8, điều này không phải là kết quả mong muốn. Với dấu ngoặc, kết quả sẽ là 2.0, vì 2 mũ 8 bằng 256.
Logarit: math.log(), math.log10(), math.log2() và logarit cơ số bất kỳ
Logarit là phép toán ngược của lũy thừa. Hàm math.log() tính logarit của một số với một cơ số nhất định. Mặc định, nó sử dụng logarit tự nhiên với hằng số e (khoảng 2.71828…) làm cơ số:
math.log(42)Để sử dụng logarit thập phân (cơ số 10), bạn có thể cung cấp cơ số dưới dạng đối số thứ hai:
math.log(42, 10)Các nhà phát triển thư viện math cũng đã tạo một phím tắt cho logarit thập phân vì nó khá phổ biến. Bạn có thể sử dụng hàm math.log10():
math.log10(42)Logarit cơ số 2 cũng rất phổ biến trong điện toán. Tương tự, có một hàm math.log2() để tính logarit cơ số 2. Để tìm số bit cần thiết cho một số, bạn có thể sử dụng hàm này:
math.log2(512)Bạn có thể sử dụng một cơ số khác bằng cách lấy logarit tự nhiên hoặc logarit thập phân của một số và chia cho logarit của cơ số bạn muốn sử dụng. Ví dụ, để lấy logarit của 81 với cơ số 3:
math.log(81) / math.log(3)Kết quả sẽ là 4.0, vì 3 mũ 4 bằng 81. Bạn có thể kiểm tra lại bằng cách lấy antilogarit (nghịch đảo của logarit) cơ số 3:
3**4
Hình ảnh máy tính khoa học với các biểu tượng Python xung quanh, minh họa Python như một công cụ tính toán mạnh mẽ thay thế.
2. Sử dụng các hằng số toán học cơ bản
Ngoài các phép toán, thư viện math cũng giúp bạn dễ dàng sử dụng các hằng số toán học quan trọng như e và pi.
Bạn có thể nhớ rằng diện tích hình tròn bằng pi nhân với bình phương bán kính. Dưới đây là cách tính diện tích hình tròn với bán kính 6 đơn vị:
import math
math.pi * 6**2Thao tác này sẽ trả về giá trị diện tích là 113.09733552923255.
3. Các hàm lượng giác trong Python
Nếu bạn thường xuyên sử dụng các hàm lượng giác trên máy tính khoa học, thư viện math trong Python cũng cung cấp đầy đủ các hàm này. Các hàm sin, cosin, tang và các hàm lượng giác ngược tương ứng đều có sẵn.
Lưu ý rằng các hàm lượng giác này hoạt động với đơn vị radian. Tuy nhiên, bạn có thể dễ dàng chuyển đổi từ độ sang radian bằng hàm math.radians(). Ví dụ, để chuyển đổi 60 độ sang radian:
import math
math.radians(60)Để tính sin của góc này, bạn sử dụng hàm math.sin():
angle = math.radians(60)
math.sin(angle)Chúng ta có thể lấy lại góc ban đầu bằng cách sử dụng math.asin(), hàm sin ngược hoặc arcsin:
math.asin(0.8660254037844386) # Giá trị sin của 60 độ đã tính ở trênTrong chế độ tương tác của Python, bạn cũng có thể sử dụng toán tử gạch dưới _ để lấy kết quả của phép tính trước đó, giúp tiết kiệm thời gian gõ phím:
math.asin(_)Cũng có một hàm để chuyển đổi từ radian sang độ:
math.degrees(_)Thao tác này sẽ đưa chúng ta trở lại giá trị đo ban đầu là 60.0 độ. Các hàm math.cos(), math.acos(), math.tan() và math.atan() cũng hoạt động tương tự.
4. Giải phương trình đại số với SymPy và NumPy
Python không chỉ thực hiện các phép tính số học mà còn có thể giải các phương trình đại số với sự trợ giúp của các thư viện chuyên dụng. Bạn không cần đến các hệ thống đại số máy tính độc quyền và đắt tiền như Mathematica hay Maple. Thay vào đó, bạn có thể giải quyết các bài toán toán học và khoa học một cách dễ dàng với Python.
Giải phương trình đại số đơn giản với SymPy
Hãy sử dụng thư viện SymPy để giải một phương trình đơn giản: 3x + 5 = 7. Mặc dù đây là một bài toán dễ giải bằng tay, nhưng nó sẽ minh họa khả năng của SymPy.
Đầu tiên, hãy import SymPy:
from sympy import *Trước khi sử dụng x, chúng ta cần định nghĩa nó là một biến ký hiệu (symbolic variable):
x = symbols('x')SymPy mong đợi các phương trình bằng 0, vì vậy chúng ta sẽ sử dụng hàm Eq() của SymPy để định nghĩa phương trình:
eqn = Eq(3*x + 5, 7)
Giao diện terminal hiển thị việc giải phương trình đại số đơn giản bằng thư viện SymPy trong Python.
Bây giờ chúng ta sẽ sử dụng hàm solve() để giải cho x:
solve(eqn, x)Kết quả sẽ là [2/3].
Nếu bạn sử dụng ứng dụng dòng lệnh isympy, nó sẽ tự động import SymPy vào môi trường tương tác, định nghĩa một số biến phổ biến bao gồm x và thiết lập hiển thị đẹp mắt (pretty printing) để kết quả trông giống như trong sách giáo khoa hơn.
Giải phương trình bậc hai với SymPy
Hãy thử một bài toán khó hơn. Một phương trình bậc hai sẽ khó giải bằng tay hơn. May mắn thay, với SymPy, bạn không cần phải nhớ công thức nghiệm bậc hai hay cách hoàn thành bình phương. Chúng ta sẽ giải phương trình bậc hai x^2 + 4x + 2 = 0. Chúng ta có thể trực tiếp giải nó cho x:
solve(x**2 + 4*x + 2, x)Các nghiệm sẽ là [-2 + sqrt(2), -2 - sqrt(2)]. Hãy nhớ định nghĩa rõ ràng phép nhân, ví dụ 4*x cho 4x.
Giải hệ phương trình tuyến tính với NumPy
Bạn cũng có thể dễ dàng giải một hệ phương trình tuyến tính với thư viện NumPy. Chúng ta sẽ giải hệ phương trình ví dụ đầu tiên từ trang Wikipedia về hệ phương trình tuyến tính:
3x + 2y - z = 1
2x - 2y + 4z = -2
-x + 1/2y - z = 0
Chúng ta sẽ sử dụng một ma trận và một vector để giải bài toán này. Chúng ta chỉ cần các hệ số của các biến. Chúng ta sẽ sử dụng một mảng 2 chiều, hay một mảng của các mảng, để biểu diễn ma trận hệ số:
import numpy as np
A = np.array([[3, 2, -1], [2, -2, 4], [-1, 1/2, -1]])Và chúng ta sẽ sử dụng một mảng khác cho vector cột của các hằng số ở phía bên phải của hệ phương trình:
b = np.array([1, -2, 0])Sau đó, chúng ta sẽ sử dụng hàm np.linalg.solve() của NumPy để giải nếu hệ có nghiệm (không phải tất cả các hệ phương trình tuyến tính đều có):
np.linalg.solve(A, b)Bạn sẽ nhận được một danh sách các nghiệm của hệ thống, trong trường hợp này là [ 1. -2. -2.]. Các giá trị này tương ứng với các biến x, y và z.
Giao diện màn hình máy tính hiển thị ứng dụng Discover trên Kubuntu Focus Ir16 (Gen 2), gợi ý các công cụ khoa học và toán học cho Linux.
5. Tính toán thống kê cơ bản với thư viện Statistics
Nhiều máy tính khoa học và bảng tính như Excel có sẵn các phép toán thống kê. Bạn cũng có thể thực hiện một số thống kê đơn giản với thư viện statistics của Python.
Hãy tạo một mảng chứa một vài số để làm tập dữ liệu của chúng ta:
data = [25, 42, 35]Để tính giá trị trung bình (mean) của một vài số, hãy đặt chúng vào một mảng và sử dụng hàm statistics.mean():
import statistics
statistics.mean(data)Để tính giá trị trung vị (median):
statistics.median(data)Và để tính giá trị mode (giá trị xuất hiện thường xuyên nhất):
statistics.mode(data)Trong trường hợp này, với mỗi số xuất hiện một lần, Python sẽ in ra số đầu tiên. Nếu có nhiều giá trị có cùng tần suất cao nhất, statistics.mode() sẽ trả về giá trị đầu tiên nó tìm thấy. Nếu muốn tìm tất cả các mode trong trường hợp có nhiều hơn một, bạn có thể dùng statistics.multimode().
6. Nhập khẩu từng hàm riêng lẻ để tối ưu hiệu suất
Trong Python, nếu bạn chỉ cần sử dụng một hoặc một vài hàm cụ thể từ một thư viện cho mục đích tương tác, bạn có thể nhập khẩu chúng trực tiếp. Điều này giúp mã của bạn gọn gàng hơn và tránh việc phải gọi tên thư viện mỗi khi sử dụng hàm.
Ví dụ, nếu bạn chỉ cần hàm sin từ thư viện math, bạn có thể nhập khẩu nó như sau:
from math import sinBây giờ bạn có thể sử dụng hàm sin() mà không cần phải gọi thư viện math trước đó:
sin(42)Cách này đặc biệt hữu ích khi bạn làm việc trong môi trường tương tác hoặc Jupyter Notebook, nơi sự ngắn gọn có thể nâng cao hiệu quả làm việc.
7. Tính toán giai thừa, hoán vị và tổ hợp
Các phép toán tổ hợp cơ bản như giai thừa, hoán vị và tổ hợp cũng có sẵn trong Python thông qua thư viện math. Đây là những công cụ không thể thiếu trong nhiều lĩnh vực toán học, thống kê và khoa học máy tính.
Đầu tiên, chúng ta cần nhập khẩu các hàm cần thiết từ thư viện math:
from math import factorial, comb, permGiai thừa (factorial())
Giai thừa của một số (n!) là tích của tất cả các số nguyên dương từ 1 đến số đó. Ví dụ, 49 giai thừa là 49!. Để tính 49!:
factorial(49)Kết quả sẽ là một số rất lớn.
Tổ hợp (comb())
Tổ hợp tính toán số cách chọn k phần tử từ một tập hợp n phần tử mà không quan tâm đến thứ tự. Để tính số tổ hợp bạn có thể nhận được khi rút 5 lá bài từ bộ bài 52 lá tiêu chuẩn:
comb(52, 5)Hoán vị (perm())
Hoán vị tính toán số cách chọn k phần tử từ một tập hợp n phần tử mà có quan tâm đến thứ tự. Để tính số hoán vị (tức là rút bài mà thứ tự quan trọng):
perm(52, 5)Các hàm này giúp bạn giải quyết các bài toán xác suất và tổ hợp một cách nhanh chóng và chính xác.
8. Vẽ đồ thị hàm số với SymPy
SymPy không chỉ có thể giải phương trình mà còn có thể vẽ đồ thị chúng, giống như cách một máy tính đồ thị thực hiện. Khả năng trực quan hóa này là cực kỳ hữu ích cho việc học tập và phân tích các hàm số.
Bạn có thể vẽ các hàm dưới dạng y = mx + b, trong đó m là độ dốc và b là điểm cắt trục y. Chúng ta chỉ cần phần mx + b. Ví dụ, để vẽ đồ thị của y = 3x + 5:
from sympy import symbols, plot
x = symbols('x')
plot(3*x + 5)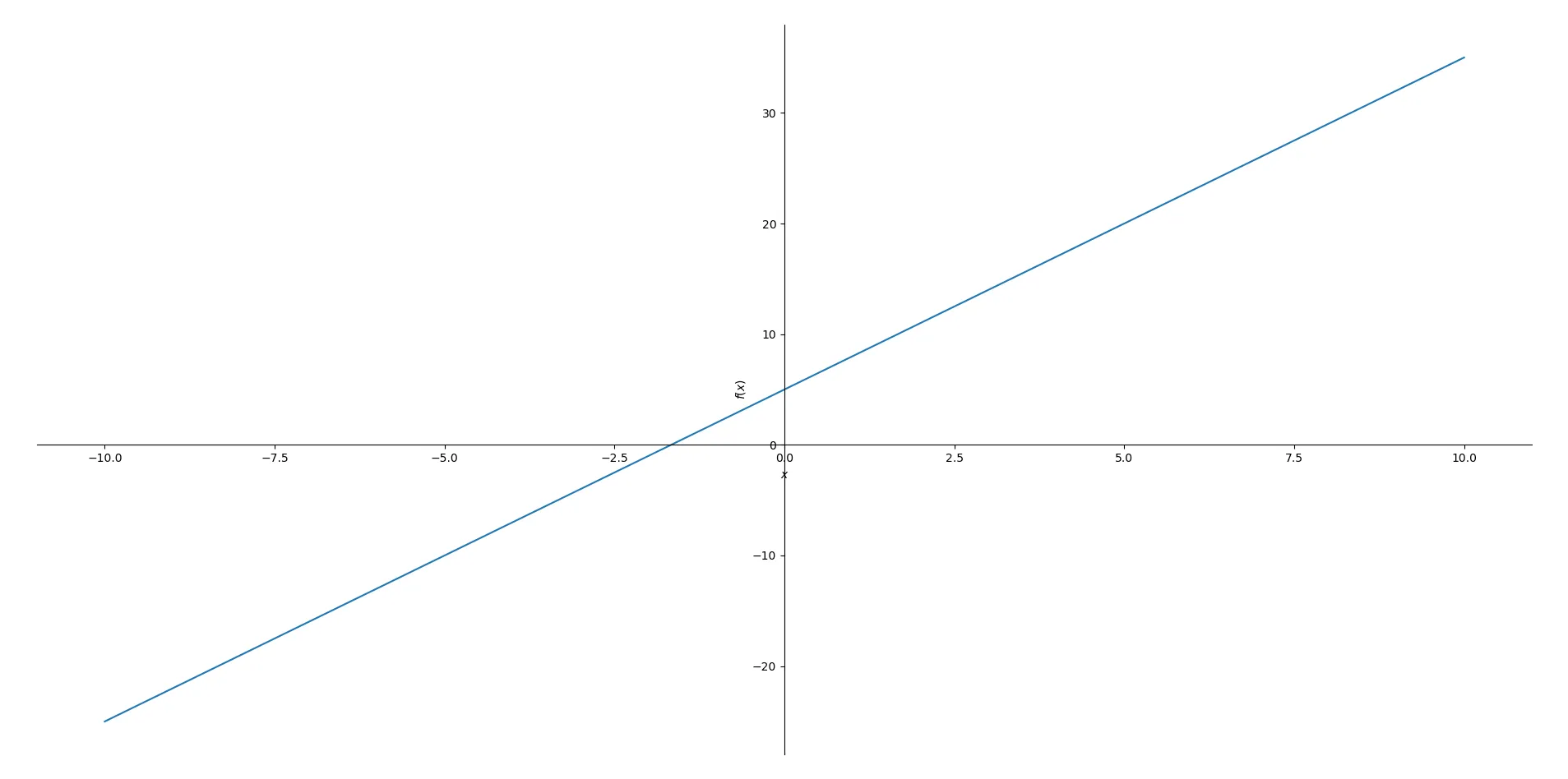
Đồ thị của một phương trình tuyến tính (y = 3x + 5) được vẽ bằng thư viện SymPy trong Python.
Một cửa sổ sẽ bật lên với đồ thị hoặc nó sẽ xuất hiện trong một Jupyter Notebook. Với tất cả các chức năng này, bạn có thể cất chiếc máy tính khoa học hoặc máy tính đồ thị cũ vào ngăn kéo và sử dụng một công cụ linh hoạt, mạnh mẽ và tiết kiệm chi phí hơn rất nhiều.
Biểu tượng Jupyter trên màn hình laptop và hành tinh Sao Mộc, minh họa môi trường Jupyter Notebook cho lập trình tương tác.
Kết luận
Qua bài viết này, chúng ta đã cùng nhau khám phá những khả năng tuyệt vời của Python trong việc biến nó thành một công cụ tính toán khoa học và đồ thị toàn diện. Từ các phép toán số học cơ bản như lũy thừa, căn bậc, logarit, đến các hàm lượng giác phức tạp, giải phương trình đại số với SymPy, hệ phương trình tuyến tính với NumPy, các phép thống kê cơ bản và thậm chí là vẽ đồ thị hàm số, Python đều thể hiện sức mạnh và sự linh hoạt vượt trội.
Việc nắm vững các thư viện math, statistics, SymPy, và NumPy không chỉ giúp bạn giải quyết các bài toán toán học và khoa học một cách hiệu quả mà còn mở ra cánh cửa đến với thế giới lập trình ứng dụng trong khoa học dữ liệu, học máy và nhiều lĩnh vực công nghệ khác. Python không chỉ là một ngôn ngữ lập trình mà còn là một bộ công cụ đa năng, giúp bạn tiết kiệm chi phí, tối ưu hóa quy trình làm việc và nâng cao năng lực tính toán.
Hãy bắt đầu trải nghiệm và ứng dụng Python vào các tác vụ tính toán hàng ngày của bạn. Chắc chắn bạn sẽ thấy Python là một sự thay thế hoàn hảo, thậm chí vượt trội so với máy tính cầm tay truyền thống.
